
Can you tell what these three word problems have in common?
- I had 8 cookies, and then I ate 5. How many cookies did I have left?
- I have 8 cookies. 5 are chocolate, and the rest are oatmeal raisin. How many are oatmeal raisin?
- There are 8 chocolate cookies and 5 sugar cookies in the cookie jar. How many more chocolate cookies are there than sugar cookies?
Yes, they’re all about cookies. But these word problems have something else in common, too. These situations feel very different from each other, but you can solve them all by subtracting 5 from 8.
Many textbooks only present subtraction as taking away. But there are actually three different interpretations of subtraction:
- Taking away
- Part-whole
- Comparison
When your child learns all three meanings, he’ll understand subtraction on a deeper level. He’ll be able to solve real-life subtraction problems with confidence, and the three meanings will even help him master the subtraction facts more easily. In this article, you’ll learn all three interpretations so that you’re equipped to teach your child this vital skill.
3 Essential Meanings of Subtraction
Taking Away
In take-away subtraction problems, items are removed in some way. Pencils are lost, cupcakes are eaten, pennies are spent, and so forth.
I had 8 cookies and then I ate 5. How many cookies are left?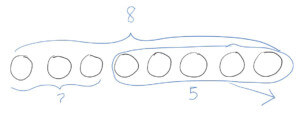
Thinking of subtraction as “taking away” makes subtraction easy to understand and concrete. That makes it the perfect way to introduce subtraction to young children. As they begin to explore subtraction, they can solve simple problems by physically “taking away” objects to find the answer.
Starting with take-away subtraction also helps children understand that subtraction is the opposite of addition. Since removing objects is the opposite of adding objects, they can concretely see and feel the difference between these two operations.
Part-whole
Part-whole subtraction problems don’t involve removing anything. Instead, you know the total number and the size of one part, and you subtract to find the size of the other part.
I have 8 cookies. 5 are chocolate, and the rest are oatmeal raisin. How many are oatmeal raisin?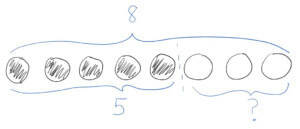
To solve part-whole subtraction problems, children don’t physically remove objects. Instead, they separate the whole group into two parts and find the size of each part. In real life, part-whole subtraction often comes up when you have a group with two smaller subgroups and you want to know how big one of the subgroups is. (For example, a flock of birds with robins and sparrows, or a class of children with boys and girls.)
Comparison
Comparison subtraction is the most challenging interpretation for most children. In comparison subtraction problems, you subtract to find out how much bigger (or how much smaller) one set is compared to another. For example, we often use comparison subtraction to tell how much more one person has compared to another: How many more toy cars does Daniel have than Jacob? Comparison subtraction also arises frequently when measuring: How much shorter is this rope compared to that rope? How much older is this person than that person?
There are 8 sugar cookies and 5 gingersnaps. How many more sugar cookies are there than gingersnaps?
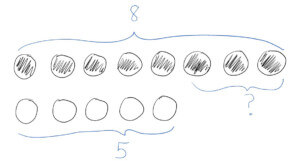 We call the answer to a subtraction problem the difference because of this comparison meaning of subtraction. When we subtract, we are literally finding out how “different” two numbers are from each other–how much greater one number is than the other.
We call the answer to a subtraction problem the difference because of this comparison meaning of subtraction. When we subtract, we are literally finding out how “different” two numbers are from each other–how much greater one number is than the other.
How to Teach Subtraction Like a Pro
Here’s how you can help your children develop a deep understanding of all three meanings of subtraction.
- Include all three subtraction meanings in your teaching. Begin with simple take-away subtraction problems with your kindergartner or first-grader. Introduce part-whole problems in the later part of first grade, and finally tackle comparison problems in second grade. This clear, gradual progression will help your child make sense of all three interpretations without feeling overwhelmed.
- When reading subtraction problems aloud, say “minus” for the minus sign and not “take away.” For example, when you read the problem 6 – 4, say “six minus four” and not “six take away four.” This helps children think more flexibly about the role of the minus sign and mentally prepares them to understand interpretations other than take-away.
- Use manipulatives to act out subtraction problems. You can use commercial math manipulatives, but simple household items like buttons, blocks, or small toys work well, too. Nothing helps children understand subtraction better than physically acting out problems with real objects.
- Word problems about unfamiliar situations can feel very abstract and difficult to children. When you’re first introducing a new subtraction meaning, keep word problem situations as relevant to your child as possible. Kids especially enjoy word problems that include their interests. For example, if your child loves soccer, you might ask questions like:
- I brought 12 juice boxes to the soccer game. The team members drank 9 of them. How many juice boxes were left? (Take-away)
- There are 10 kids on the team. Six of them are girls. How many are boys? (Part-whole)
- My team scored 7 goals, and the other team scored 5 goals. How many more goals did my team score? (Comparison)
- When your child solves numbers-only problems (as opposed to word problems), encourage her to use whichever subtraction meaning makes the problem easiest to solve. For example, take-away subtraction is best suited to problems like 12-3 which involve subtracting a small number. On the other hand, comparison subtraction is very helpful for problems like 9 -7 where the two numbers are close together. These strategies will help make mastering the math facts much more manageable for your children.
Recommended Products
-

Juneteenth Booklist & Activities
0 out of 5$0.00 Add to cart -


Fifth Grade Math with Confidence Instructor Guide
0 out of 5Starting at:$36.95Original price was: $36.95.$27.71Current price is: $27.71. Select options -
Sale!

Hansel & Gretel and Other Stories: Downloadable MP3
0 out of 5$12.95Original price was: $12.95.$8.42Current price is: $8.42. Add to cart -
Sale!

Dorothy and the Wizard in Oz: Downloadable MP3
0 out of 5$25.95Original price was: $25.95.$16.87Current price is: $16.87. Add to cart -
 Sale!
Sale!

Fifth Grade Math with Confidence Student Workbook B
0 out of 5$16.46 – $21.56 Select options This product has multiple variants. The options may be chosen on the product page -
 Sale!
Sale!

Fifth Grade Math with Confidence Student Workbook A
0 out of 5$16.46 – $21.56 Select options This product has multiple variants. The options may be chosen on the product page
ABOUT THE AUTHOR
Kate Snow
Join over 100,000 homeschooling families
For the latest offers, educational insights, products and more.
By joining you agree to our privacy policy.



















10 thoughts on “Subtraction: More Than Just Taking Away”
Very informative. One take away (pun intended) has me thinking about part to whole where you stated kids arentntaking anything away. Consider this, if there are 128 people in a team and 37 are boys, how many are girls? One would need to use subtraction to find the answer. I understand what you’re saying in the big idea and how it’s different than “take away” but you’re still taking away or subtracting the boys from the total to find the answe.
Love this article!
this will help my kids how to subutration numbber
Very good article helped too much ! Thank you !
Great observation! It’s easy to forget how different those contexts are when we are trained to focus on just the numeric aspects of the problem.
(Of course, it is also nice to know that subtraction solves all three of those problems!)
Very helpful information on subtraction!! Great strategies!
I have a great understanding of addition and subtraction but it’s been difficult for me to explain this to my kids. I feel like I’m doing a great job but they don’t see it that way, haha. I like these tips and while I knew these were different I didn’t really know there were 3 different types of subtraction. They all make sense to me and will certainly add this to our curriculum. Thank you!
I really enjoyed this post! It’s fascinating to see how subtraction can be viewed through different lenses beyond just taking away. The examples you provided helped clarify the concept, especially in real-life scenarios. Looking forward to more insights on mathematical operations!
I loved how this post highlighted the importance of viewing subtraction as more than just taking away. The real-world examples really made the concept come alive for me! It’s fascinating to see how essential subtraction is in various situations, not just in math class. Thank you for sharing such an insightful perspective!
This was such a refreshing take on subtraction! I never realized how much depth there is to this basic operation. The examples you provided really helped illustrate how subtraction plays a role in problem-solving beyond just taking away. Great read!